无所不能的奇偶数

无所不能的奇偶数

作者：焦述铭，鹏城实验室

想必大家都知道什么是奇数和偶数，整数中能被2整除的是偶数，反之就是奇数，偶数包括0，2，4，6，……这些双数，奇数包括1，3，5，7，……这些单数。不过表面上看似平白无奇的奇偶数，其实“暗藏玄机”，在很多意想不到的时候都可以助你一臂之力。

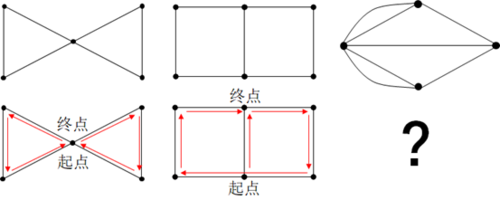
不少人小时候都玩过“一笔画”游戏，规则是笔不能离开纸面，起点终点任选，从起点一路画到终点，每条线都要走过，但又不能重复走第二次，当然每个节点是可以反复穿过的。对于下面左中右三个图形，可以试下，是否能够一笔画出来？左侧和中间的“蝴蝶结”和“横八字”图形，应该是“小菜一碟”的任务，参考答案也画在了下方。可是对于右侧第三个图形，恐怕是遇上硬骨头了，用尽浑身解数，怎么试也不会成功。实际上这第三个图形就是著名的“七桥问题”，七条线相当于七座桥，想一次性不重复地走完七座桥是不可能的。

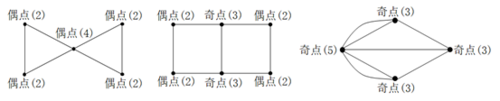
那么什么样的图形可以一笔画出来，什么样的不能？奇偶数就是幕后的支配者。图中如果某个节点连接的线条数为奇数条，称为奇点；如果某个节点连接的线条数为偶数条，称为偶点。一笔画规律是：只有图中具有0个或2个奇点的图，才可以一笔画成。上面三个图形中各个节点的线条数，以及属于奇点还是偶点，在标注了之后（如下图），就一目了然了。第一个“蝴蝶结”图中有0个奇点，第二个“横八字”图中恰好有2个奇点，都满足上述条件，可以一笔画出来，而第三个图中有多达4个奇点，自然不符合一笔画的条件。

以上所说的规律又是怎么得到的呢？在一笔画的过程中，所有的节点可以分为一个起点，一个终点，其它中途点这三类。中途点到达了一次之后，也必须离开一次，所以无论是“一面之交”，还是“多次拜访的老朋友”，必须要是偶点，而起点允许有一次“一去不复返”，出发后就不再返回，终点允许有一次“落叶归根”，到达后就不再出发，这样起点和终点可以“破例”成为2个奇点（如“横八字”图），但如果起点和终点是重合的，这一个点也会和其它中途点一样成为偶点，也就是0个奇点的情形（如“蝴蝶结”图）。而像“七桥问题”中有四个节点全部是奇点，实在让人勉为其难，起点和终点怎么样也不需要有那么多个，于是“七桥问题”成为了无解的一笔画难题。

现实中一笔画不仅仅是个游戏，还属于计算机图论专业研究范围，在物流，运筹，交通，网络通信，社交关系结构中都发挥重要作用，比如一个快递小哥选择怎样最方便的路线，才能“不走回头路”地送完所有邮件。

除了一笔画之外，奇偶数还有一个更加神奇的本领，可以帮你“心灵感应”，读出别人的心思，你相信吗？我们从一个简单的扑克牌魔术说起。魔术师首先把16张扑克牌正面朝上摆成一个阵列（如左上方图a所示），其中9张是黑色，都摆在了一起，剩下7张是红色，摆在了外围一圈。接下来找三位观众上台，在交代了每位观众需要做什么之后，魔术师就背对大家，对于接下来发生的事情“毫不知情”。首先第一位观众选择任意数量黑色牌翻过去，负责把黑色牌正面朝上还是背面朝上打乱（达到右上方图b的效果），但规定不能动红色牌。然后轮到第二位观众选择任意数量红色牌翻过去，负责把红色牌正面朝上还是背面朝上打乱（达到左下方图c的效果），但规定不能动黑色牌。最后第三位观众在所有的十六张牌中选一张，再翻一下，原本正面朝上就变成背面朝上，原本背面朝上就变成正面朝上（达到右下方图d的效果，例如黑桃2被翻了）。此时魔术师再转过身来，他说自己并没有看到刚刚发生的一切，但凭借第三位观众留下的蛛丝马迹，就能猜出最后哪张牌被动过了，并成功指出是黑桃2.。

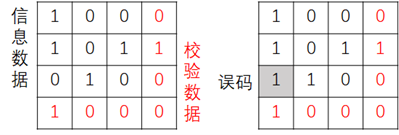
那么魔术师是怎么做到的呢？可以提示一下大家，三位观众中有一位是“托儿”，你能猜出来是哪位吗？正确答案是第二位观众。而魔术师事先也仅仅和这位观众做了一个简单的约定，就是尽管他只能翻红色的牌，但要假装随意翻的，实际有意地保证每一行和每一列中正面朝上牌的个数都是奇数张（1张或3张），而不是偶数张，大家可以从左下方的图里再次确认下是不是这样。之后第三位观众无论翻了16张中的哪一张，都会破坏奇数张的规律，造成某一行和某一列正面朝上牌的个数变为偶数张，魔术师从这一行和列的交叉点位置就可以找出最后被动过的牌。

这同样不仅仅是一个简单的扑克牌魔术，在现在计算机，互联网和通信中，各种信息都表示为了大量的二进制的1和0数据，如果扑克牌正面朝上和背面朝上分别表示1和0，每张牌相当于一个比特，那么9个比特的黑色牌可以表示实际要储存或者传输的数据，7个比特的红色牌相当于外加的校验数据，通过这种“奇偶校验”，当16个比特中任何一个出错的时候（相当于被第三位观众翻过来的“误码”），接收方就可以检测并纠正过来，整个过程称为“信息纠错编码”。当然奇偶校验只是其中最简单的一种方式，还有其它很多更加精巧设计的复杂信息纠错编码方式。

我们平时在超市购物所使用的条形码，还有移动支付和社交小程序使用的二维码，里面的黑白线条或者黑白方块就表示了大量的1和0，为了应对扫码读码时可能出现的错误，其中也都使用了信息纠错编码，一个二维码不清晰了，扭曲变形了，甚至部分区域被一个头像遮挡住，还是可以正确读取信息。

奇偶数还可以用来表演另外一个魔术，下面左侧和中间两张”胡椒”的图片，是不是看起来一模一样，你能观察到有任何的分别吗？但诡异的是，左侧胡椒图片一切正常，无法提取出信息，中间胡椒图片却“另有乾坤”，可以从中提取出右侧的密码信息。这称为图像信息隐藏（或隐写），又是怎样做到的呢？

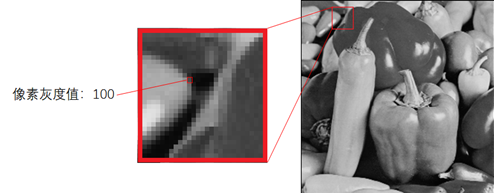
在计算机上，每张照片或者图像放大了之后，都会像马赛克一样，是由一个个小方块组成的，每个小方块称为一个像素。而单个像素的明暗程度或者颜色可以用数字来表示，比如在一张黑白照片（专业称灰度照片）中，可以用0到255中间某个数字表示灰度深浅，0表示全黑色，255表示全白色，之间的数值则表示从黑色，深灰色，中灰色，浅灰色，一直到白色的逐渐过渡。如果两个像素的灰度值只相差1，表示颜色非常接近，人眼实在难以分辨。而如果是彩色图片，则要用三个数字表示一个像素，分别表示红绿蓝三原色的深浅。

正常来说，每个像素的灰度值是奇数还是偶数是随机的，碰巧决定的，如果人为通过加1或者减1，把一些像素的灰度值做稍微更改，就可以让奇数和偶数像素值的排列不再随机和无意义，而是表示要隐藏的信息。如上所说，各种信息都可以用二进制的1和0表示，一个像素灰度值如果是奇数，就表示1，偶数就表示0，这样每个像素可以表示一个隐藏的比特，一整张处理后的图片就可以隐藏着大量信息，并且图片本身发生的改动还微乎其微，很难察觉出来。

图像信息隐藏在保密通信，版权保护，军事情报，文件票据防伪等场景中有很多的应用。例如一位作者自己创作了一幅画或者一段视频作品，公开上传后，被别人抄袭，结果脸皮厚的抄袭者还反过来声称作品是自己先创作的，真正作者才是抄袭的一方，原作者如果事先在作品中把个人信息隐藏进去，就可以作为证据，证明自己才是真正的版权拥有者。而如果一份保密文件只能在十个人内部传阅，不得泄露外传，可以将分发给每个人的文件分别隐藏进不同信息作为标记，当有人违反规定将文件外传之后，可以根据外传的文件中隐藏的信息判断出谁是“内鬼”。

奇数和偶数看似简单，却又不简单，通过巧妙的设计，可以在计算机图论、信息编码、图像信息安全等各种任务中大显身手，无所不能的表现简直超乎想象。